
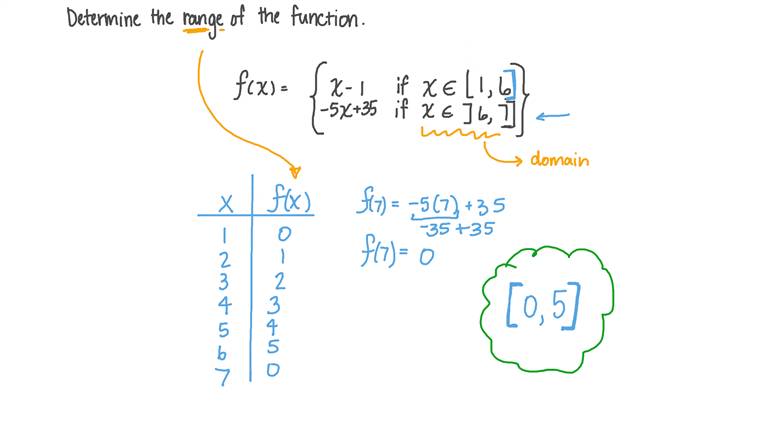
Since f(x) = 1 when x = 0, we plot a filled point at (0,1). Make sure to leave the point of origin unfilled. Just make sure that the two points satisfy y = 2x. To graph the linear function, we can use two points to connect the line. Using the graph, determine its domain and range.įor all intervals of x other than when it is equal to 0, f(x) = 2x (which is a linear function).
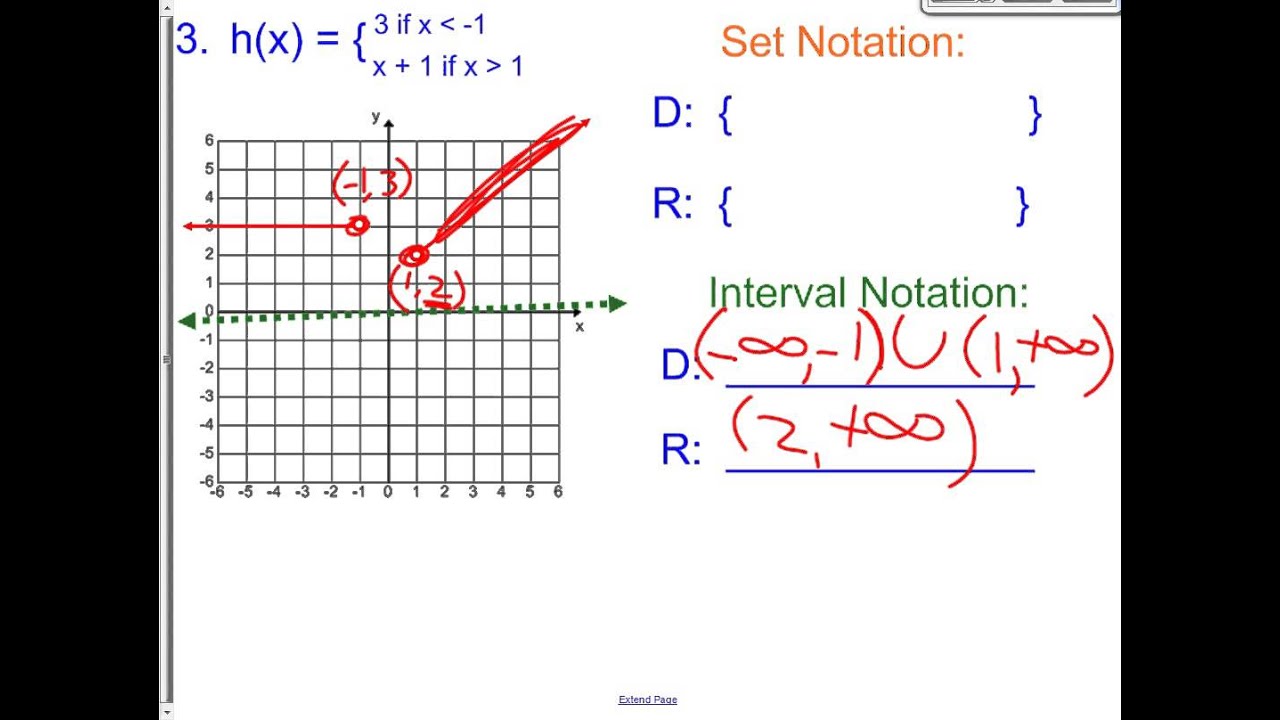
Graph the piecewise function shown below. Let’s evaluate f(49) using the expression.

Let’s evaluate f(-36) using the expression. When x = -36 (or less than 0), the expression for f(x) is x/6.2x, for x 0, x = 0, and x 0, f(x) is equal to 2x. The function is defined by pieces of functions for each part of the domain. Piecewise function definitionĪ piecewise function is a function that is defined by different formulas or functions for each given interval. To fully understand what piecewise functions are and how we can construct our own piecewise-defined functions, let’s first dive into a deeper understanding of how it works. Graphing and interpreting piecewise functions.
#Piecewise function domain and range calculator how to
Learning how to evaluate piecewise-defined functions at given intervals.In this article, you’ll learn the following: This is why we’ve allotted a special article for this function. Tax brackets, estimating our mobile phone plans, and even our salaries (with overtime pay) make use of piecewise functions. We actually apply piecewise functions in our lives more than we think so. Piecewise functions are defined by different functions throughout the different intervals of the domain. When this happens, we call these types of functions piecewise-defined functions. There are instances where the expression for the functions depends on the given interval of the input values. Piecewise Functions – Definition, Graph & Examples


 0 kommentar(er)
0 kommentar(er)
